2.1.1 流量连续性方程（质量守恒方程）
质量守恒方程可以表述为单位时间内的流体微元体质量的增加等于相同时间内流入该流体微元的体的净质量[5]。
在流体通道中有流体流入同时也会伴随一部分流体流出，在此期间该流体通道中的质量也会发生变化。
那么根据质量守恒定律，单位时间内从出风口流出与从进风口流入干燥段的热空气质量差之总和应等于干燥段内因密度变化而减少的质量，即：
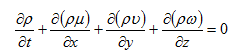（2.1）
式中：ρ为热空气密度，kg/m3；用 μ、ν、ω分别代表热风流体在x、y、z方向作为质点的速度V的分量，m/s。
2.1.2 流体运动方程（动量守恒定律）
在流体微元体中，流体的动量对时间的相对变化率等于外界作用在微元体上各种力的和，称为动量方程[6]。即在一个流体微元中动量的变化率等于流入流体微元体的动量通量之和减去流出流体微元体的动量通量之和，同时还要加上作用在流体微元体上所有剪切力、法向应力和作用其质量上的力。即：
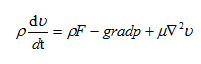（2.2）
式中：ρ为热空气流体密度，kg/m3；V为热风速度，m/s；F是质量力，N；是哈密顿算子；为热风速度变化率。质量守恒方程可以表述为单位时间内的流体微元体质量的增加等于相同时间内流入该流体微元的体的净质量[5]。
在流体通道中有流体流入同时也会伴随一部分流体流出，在此期间该流体通道中的质量也会发生变化。
那么根据质量守恒定律，单位时间内从出风口流出与从进风口流入干燥段的热空气质量差之总和应等于干燥段内因密度变化而减少的质量，即：
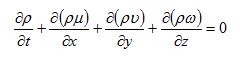（2.1）
式中：ρ为热空气密度，kg/m3；用 μ、ν、ω分别代表热风流体在x、y、z方向作为质点的速度V的分量，m/s。
在流体微元体中，流体的动量对时间的相对变化率等于外界作用在微元体上各种力的和，称为动量方程[6]。即在一个流体微元中动量的变化率等于流入流体微元体的动量通量之和减去流出流体微元体的动量通量之和，同时还要加上作用在流体微元体上所有剪切力、法向应力和作用其质量上的力。即：
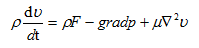（2.2）
式中：ρ为热空气流体密度，kg/m3；V为热风速度，m/s；F是质量力，N；▽是哈密顿算子；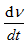
为热风速度变化率。
2.1.3 能量方程
处于流动中的流体系统总能量变化率等于外力对该系统做功功率与外界对该系统传热功率之和[7]。即：
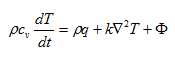（2.3）
式中：ρ为热空气流体密度，kg/m3；k为热传导系数；q为热源项；cv是定容热容；为热风温度变化率。
